統計学の解説本やサイトなどではほとんどの場合、検定方法の解説で難解な数式が載っています(Σとか√とか・・・)。
数式を見た瞬間、「ああ、これは僕(私)とは縁が無かった世界だな・・・」と本やブラウザを閉じそうになる気持ち、よくわかります。
僕も統計学が苦手でしたが、医師になってから必要に迫られてとにかく本を読みあさり、少しずつ学びました。
ですが、たくさんの統計の本を読んでわかったことは、ぶっちゃけ数式は理解できなくても困らない、ということです。
そもそも自分で研究するときも、統計解析ソフトにデータをぶち込めば結果が出ます。
ただし、統計ソフトは、どんな検定法を選ぶべきか?、この結果から何が言えるのか?ということは教えてくれません。
なのでどうしても統計学の理論については知っておく必要があります。
また論文を読むときにも、基本的な検定法とその周辺知識を持っているだけで、より深く論文の内容が理解できます。
統計学(というか数学)が苦手で、数式無しで論文の読み書きに必要な統計の知識を学びたいという人に向けた記事です。
ここでは
- 平均値と中央値
- SD(標準偏差)とIQR(四分位範囲)
- t検定とMann-Whitney U検定
について解説していきます。
目次
正規分布しているかどうかで使うべき検定法などが変わる
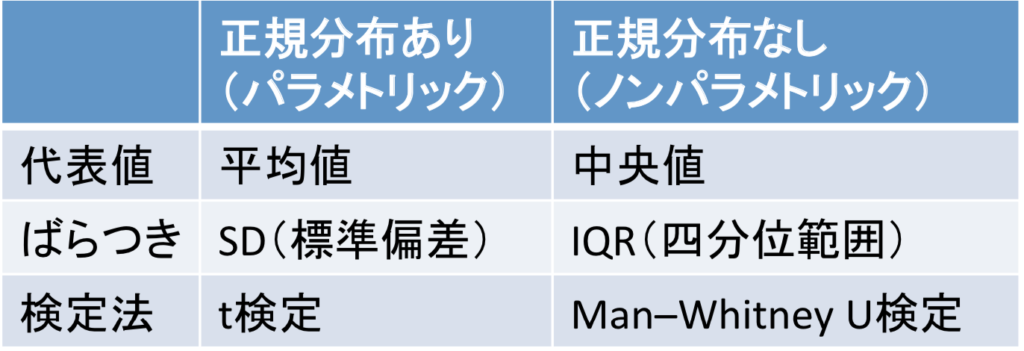
まずはこの表を見てください。
連続変数を扱う場合には、その変数が正規分布(パラメトリック)かそうでないかで使うべき検定法などが変わります。
連続変数って何だっけ?・・・
例えば、クラスの平均点とか、白血球数とか、BNP値、など数字で表されるものは連続変数です。
一方で、死亡と生存、合併症の発生の有無、のように「有り」・「無し」で評価するようなものはカテゴリー変数と言います。
正規分布ってなんだっけ?・・・
大丈夫です、全然難しくないです。
下の図の左側が正規分布です。

「平均値」を中心に左右対称で、教会にあるベルのような形をしていることから、「ベルカーブ(bell curve)」ともよばれたりします。
わかりやすい例としては、学校の定期テストや予備校の模擬試験などは正規分布(平均点付近に最も多く分布する)する傾向があります。
というかそうなるように試験問題を設計しています。
一方で臨床試験で扱う変数は必ずしも正規分布するとは限りません。
むしろ非正規分布となる変数の方が多かったりします。
なので、この違いによる統計的な取り扱いの違いを理解しておくことがとても重要なのです。
平均値と中央値
非正規分布:中央値
集団を代表する値として、平均値と中央値の違いを理解しておきましょう。
結論から言うと正規分布していれば平均値、非正規分布であれば中央値を使います。
平均値は全ての数を合計して、全体の数で割ったものです。
これはほとんどの人が知ってますよね。
中央値は最初から数えてちょうど真ん中にあたる数のことです。
例えば、全体が15個ある場合は8番目の数が中央値になります。
全体が偶数の場合は「真ん中の数字2つの平均」になります。
一番イメージしやすいのは日本人の貯金額の平均値と中央値の違いです。
金融広報中央委員会が実施した「家計の金融行動に関する世論調査(2018年)によると、20代単身世帯の貯金額の平均値は239万円です。
一方、同集団での中央値は85万円です。
かなりの差がありますよね。
平均値は正規分布(真ん中が一番多い)の集団では代表値となります。
一方で貯金額のように一部の人が高額で、圧倒的多数が0に近い値をとるような(正規分布でない)場合、中央値の方が代表値として適切です。
ちなみに論文にはいちいち、この変数は正規分布しています、とか明記されていることはほぼありません。
中央値(median)が記載されている、ということはこの変数は非正規分布が前提なんだな、と理解すれば良いです。
SD(標準偏差)とIQR(四分位範囲)
非正規分布:中央値(第1四分位−第3四分位)
「SD(標準偏差)」とか聞くとなんかもうややこしそうな感じしちゃいますが、これも全然大丈夫です。
要は値のばらつきがどれくらいかを表してるだけです。
よくある間違いで、論文のTable1(baseline characteristics)で「年齢±〇〇」とか「年齢(◯−◯)という数値を見て、「最大値と最小値」だと勘違いしてしまう人がいますが、これは違います。
正規分布をしている変数であれば「平均値±SD」で表記することが一般的で、この範囲が全体の68.26%にあたることを意味します。
ちなみに「平均値±2SD」であれば95.44%が含まれます。
外れ値を表す時に「2SDを超えている」なんて表現を聞いたことがあるかもしれません。
IQR(四分位範囲)は非正規分布のばらつきを表すために用いられます。
小さい値から順番をつけていって、
1/4番目となる値が第1四分位(25%パーセンタイル)
2/4番目となる値が第2四分位(50%パーセンタイル=中央値)
3/4番目となる値が第3四分位(75%パーセンタイル)
となります。
IQRは第1四分位–第3四分位で表します。
したがって、代表値とばらつきの表記は
中央値(第1四分位−第3四分位)と言う表記になります。
t検定とMann -WhitneyのU検定
非正規分布:Mann-WhitneyのU検定
t検定は学生時代にも聞いたことあると思いますが、Mann-Whitney U検定はどうでしょうか?
なんか医学論文ではよく見る気もするけど、イマイチよくわからない・・・
ていうかt検定もそもそもよくわからない、という人も大丈夫です。
t検定とMann-Whitney検定は、連続変数について検定するための手法です。
最初にも説明した通り、クラスの平均点とか、白血球数とか、BNP値、など数字で表されるものは連続変数です。
t検定は正規分布を前提とした検定です。
ですが臨床データの中には当然正規分布しない変数も多くあります。
非正規分布の連続変数の検定に用いられるのがMan-Whitney検定です。
そして、死亡と生存、合併症の発生の有無、のように「有り」・「無し」で評価するようなものはカテゴリー変数です。
カテゴリー変数の検定についてはカイ二乗検定とFisher正確検定を使います。
まとめ
医学論文を読む・書くに必要な統計学の知識について、数式を使わずに解説しました。
今回は連続変数の取り扱いを中心に解説しました。
カイ二乗検定や多変量解析などについてはまた別の記事で解説していきます。







