40代男性の発熱患者が来院
指導医「じゃあ問診と身体診察をしよう!」
研修医「わかりました!」
(・・・問診とかめんどいし、さっさとインフルの検査したらいいんじゃないの?)
忙しい救急外来などでついつい検査に走りたくなる気持ち、よくわかります。
ですが、インフルエンザに限らずやみくもに検査を出すと、その結果に振り回されて余計に忙しくなることだってあります。
臨床推論は初期研修の中で習得すべき項目の中でも重要度が高いです。
ここが理解できていなければ、いくら症例経験を積んでも伸び悩む可能性があります。
ここでは
- 検査前確率・尤度比・検査後確率を理解して、検査・治療の適応を考えることができる
- 検査閾値、治療閾値の概念を理解し、Clinical Decision Rule(CDR)を活用できる
ことを目標に、臨床推論の基本を一からお話しをしていきます。
少し長めの記事ですが、本を1冊読むよりははるかに短時間で読めます。
目次ごとに休憩するつもりで少しずつ読み進めてください。
目次
検査前確率とは

検査前確率とはその名の通り、“検査を全く行なっていない段階で目の前の患者がその疾患である確率”です。
全く情報が無い時点では有病率と同じになります。
ざっくりまとめると
- 病歴/身体所見から臨床医の経験に基づいて総合的に判断する
- 病歴/身体所見から文献的に検査前確率がわかるものもある(Clinical Decision Rule:CDR)
- 季節や地域、施設の性質が影響する
という感じです。
この検査前確率がどの程度か、そして検査によってどう変化するかが重要になります。
その確率によって検査・治療を判断する閾値モデルについて解説していきます。
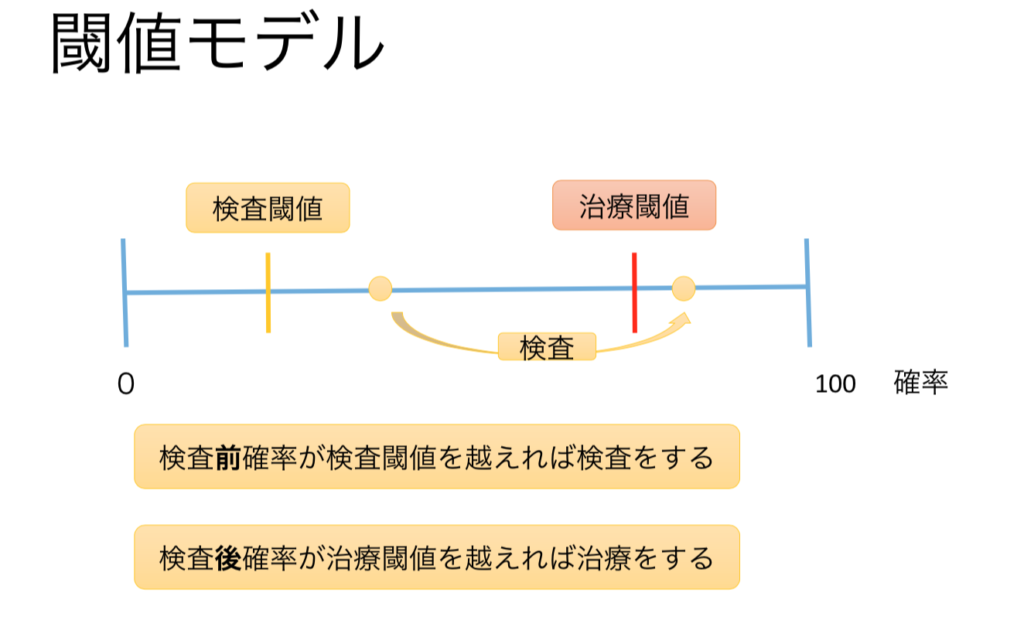
検査前確率が検査閾値を越えれば検査をします。そして検査後確率が治療閾値を越えれば治療する、というのが基本です。
インフルエンザの検査を例に挙げるならば、
という状況であれば、そもそもインフルエンザを疑っていないので「検査前確率が検査閾値を超えない」(つまり検査しない)、という状態です。
この検査閾値・治療閾値をどう考えるかは後で解説するので少し待ってください。
では検査によって、どれくらい確率が変化するかを考えるために必要な尤度比とオッズについて説明していきます。
尤度比とオッズ

検査が陽性(または陰性)のときにどのくらい検査後確率が変化するかを表すのが尤度比です。
- 陽性尤度比=感度/(1−特異度)
- 陰性尤度比=(1−感度)/特異度
この尤度比は検査の特性を表すのに便利なのですが、そのまま検査後確率を計算することはできません。
「確率」を「オッズ」に置き換えてベイズの定理を使って計算していきます。
検査前オッズ×尤度比=検査後オッズ
なんか計算とかめんどくさそう・・・と思うかもしれませんが、毎回計算する必要は無いので安心してください。
最近は検査後確率をすぐに計算できるアプリなんかもあります。
あくまでも理論を理解するために一度は計算の過程を見ておくことが重要です。ここだけなんとかがんばってください。
確率をPとするとオッズ=P/1-P と表すことができます。なので
検査前オッズ=検査前確率/(1-検査前確率)
となります。ここまではむずかしく無いですよね?
この検査前オッズに尤度比をかけて計算した検査後オッズを最後に確率に戻せば検査後確率になるわけです。
さすがにちょっとめんどくさいかなと僕も思いはじめましたが・・・大丈夫です!
ここからはインフルエンザの迅速検査を例に実際に計算をしていきます。
インフルエンザの検査を例に検査後確率を計算してみる
インフルエンザ迅速検査の感度・特異度をup to dateなどで調べたところ感度62.3%、特異度98.2%でした。
そこから尤度比をそれぞれ計算すると、
陽性尤度比:34
陰性尤度比:0.4
となりました。
陽性尤度比がめちゃくちゃ高いものの、陰性尤度比はそれほどでも無いという感じです。
ここから計算していくのですが、尤度比からだいたい検査後確率がどれくらい変化するかを推定することもできます。
それが次の表です。

これも使いつつ、症例の中で考えていきましょう。
36歳男性
会社でインフルエンザが流行している
来院当日の朝から発熱、咳、鼻水、咽頭痛、関節痛あるため受診。インフルエンザの検査希望あり。
さて、この人がインフルエンザである検査前確率はどれくらいと見積もりましょうか?
だいたいで大丈夫です。
感覚的にはほぼインフルエンザですよね?なのでここでは80%くらいとします。
先ほどの表を使って考えてみると
迅速検査陽性:80%→100%
迅速検査陰性:80%→60%
くらいになりそうです(だいたいで大丈夫です)。
なので迅速検査陰性だとしても60%くらいインフルエンザの可能性が残ります。
もしもこの状況で「検査陰性だからインフルエンザじゃない」としてしまったら・・・
元気な若者であればインフルエンザを見逃しても治療は不要なので問題にはなりにくいですが、リスクがある人では話が変わります。
リスクがある人で、検査前確率が高いのであれば、検査をせずに治療を開始することを検討すべきです。
これは閾値モデルで表現すると「検査前確率が治療閾値を超えている」、という状態です。
別の症例を考えてみましょう。
20代女性
周囲では手足口病が流行している。発熱、咽頭痛、関節痛、手足に痛みを伴う皮疹があり救急外来受診
この人がインフルエンザである確率ってどれくらいでしょうか?
ほぼ0に近いと言ってもいい気がしますが、ここでは1%としましょう。
閾値モデルでいうと「検査前確率が検査閾値を超えない」ので、実際にはこの状況でインフルエンザの検査はしないことがほとんどだと思いますが、ここではあえて検査したとします。
実際にベイズの定理を使って計算してみます。
陽性尤度比 34
検査後オッズ=検査前オッズ×尤度比
=1/99 × 34
=1/3
検査後確率 =1/4→25%
検査陰性の時の計算は明らかに0%に近いので省略しますが
検査陽性:1%→25%
検査陰性:1%→0%
となり、検査陽性でもさすがにインフルエンザとは言えないよね、という解釈になります。
でも「実際には検査前確率が何%かなんて正確にはわからないですよね・・・」と思われるかもしれません。
実は病歴や身体所見にもそれぞれ感度・特異度・尤度比が分かっているものがあって、それを解説した本が「マクギーのフィジカル診断学」です。
ここに書かれている全ての数値を覚える必要はありませんが、疾患ごとに重視すべき病歴・身体所見が数値化されているので、一度は読んでその感覚をつかんでおくことが重要です。
僕が持っているのは第2版ですが、最新版(2019年5月発売:第4版)にはPC・スマホで読める電子書籍と検査後確率を素早く計算できるEBM Calculatorがついている(おそらくスマホアプリ?)らしいので、買うなら最新版がおすすめです。
ここからは検査閾値や治療閾値について、閾値モデルの考え方をもう少し掘り下げていきます。
閾値モデル|検査閾値・治療閾値の考え方

検査閾値・治療閾値は様々な要因によって影響を受けますが、例えば、
- 疾患の緊急度・重症度
- 検査・治療のコスト
- 治療の効果
- 検査・治療に伴う合併症
などから相対的に判断していきます。
検査のコスト、合併症が大きい→検査閾値上がる
検査のコスト、合併症が小さい→検査閾値下がる
疾患の緊急度が高い:治療しないデメリットが大きい→治療閾値下がる
治療の副作用が大きい:治療のデメリットが無視できない→治療閾値上がる
もう少しイメージしやすくするために敗血症と悪性腫瘍を例に考えてみましょう。


図はあくまでもイメージですが、敗血症の場合に血液培養採取するデメリットは少ないですよね。
なので検査閾値低めになります。
そして治療しない(遅れる)デメリットが大きいのと、治療のデメリットが大きくない(抗菌薬の副作用や耐性菌の問題はありますが)ので、血液培養の結果を待たずに治療開始することは普通です。
つまり治療閾値は低いということになります。
一方で悪性腫瘍の治療閾値について、化学療法のデメリットは大きい、かつ治療開始が遅れるデメリット少ないです、つまり治療閾値高くなります。
確定診断がつかないのに化学療法なんてできないですよね。
ここまでのお話はなんとなく分かっていただけたんじゃないかと思うのですが、一方で
「閾値モデルは分かったけど、検査閾値とか結局は経験をつまないとわからないってことか・・・」
と思われるかもしれません。
それは事実なのですが、一部はこのモデルをアルゴリズム化し、科学的に検証されたものがあります。
それがClinical Decision Rule(CDR)と呼ばれるものです。
CDR:閾値モデルを定式化
肺塞栓症の診断におけるWell’s criteriaは有名ですよね。
これは病歴・身体所見などからリスクを評価し、低リスクかつDダイマー陰性なら肺塞栓を除外できる、というものです。
これはまさに、検査前確率を評価し、検査(Dダイマー)によって検査後確率が変化するという考えに元づいて作られています。


「Well’sスコアが低リスクで、Dダイマー陰性ならば検査後確率が造影CTの検査閾値を超えない」という少し複雑な構造になっていますが、図を見てもらえばイメージできるかと思います。
他にも画像検査の検査閾値を検証したものとして
- Otawa SAHルール
- Otawa 足関節ルール
- PECARN 小児頭部CTルール
- NEXUS 頚椎CTルール
なんかがあります。
これにあてはまらなければ画像検査の検査閾値を超えない(検査しなくて良い)という使い方ですね。
まとめ
臨床推論の基本について、検査前確率・尤度比から検査後確率を考える方法について解説しました。
検査前確率、検査閾値の設定は経験によるところも大きいので、自分なりに考えつつ指導医のやり方を盗んでいきましょう。
文献的にわかっている検査前確率・検査閾値をアルゴリズム化したClinical Decision Ruleを積極的に利用しましょう。
今回お話しした内容は「考える技術」という本の総論部分でより詳しく解説されています。
臨床推論について学ぶために初期研修医の先生にとって必読の一冊です。
できれば研修医1年目が終わるまでに一度読んでおき、2年目ではそれを実践していきたいところです。










